Thuật toán Prim

Trong hướng dẫn này, bạn sẽ tìm hiểu cách hoạt động của Thuật toán Prim. Ngoài ra, bạn sẽ tìm thấy các ví dụ làm việc của Thuật toán Prim trong C, C ++, Java và Python.

Thuật toán của Prim là một thuật toán cây bao trùm tối thiểu lấy một đồ thị làm đầu vào và tìm tập con của các cạnh của đồ thị đó

tạo thành một cây bao gồm mọi đỉnh
có tổng trọng lượng tối thiểu trong số tất cả các cây có thể được hình thành từ biểu đồ

Cách hoạt động của thuật toán Prim

Nó thuộc một loại thuật toán được gọi là thuật toán tham lam tìm điểm tối ưu cục bộ với hy vọng tìm ra điểm tối ưu toàn cục.

Chúng tôi bắt đầu từ một đỉnh và tiếp tục thêm các cạnh có trọng số thấp nhất cho đến khi đạt được mục tiêu.

Các bước thực hiện thuật toán của Prim như sau:

Khởi tạo cây bao trùm tối thiểu với một đỉnh được chọn ngẫu nhiên.
Tìm tất cả các cạnh nối cây với các đỉnh mới, tìm giá trị nhỏ nhất và thêm nó vào cây
Tiếp tục lặp lại bước 2 cho đến khi chúng ta có được một cây bao trùm tối thiểu

Ví dụ về thuật toán Prim

Bắt đầu với đồ thị có trọng số

Chọn một đỉnh

Chọn cạnh ngắn nhất từ đỉnh này và thêm nó

Chọn đỉnh gần nhất chưa có trong lời giải

Chọn cạnh gần nhất chưa có trong lời giải, nếu có nhiều lựa chọn, hãy chọn một cách ngẫu nhiên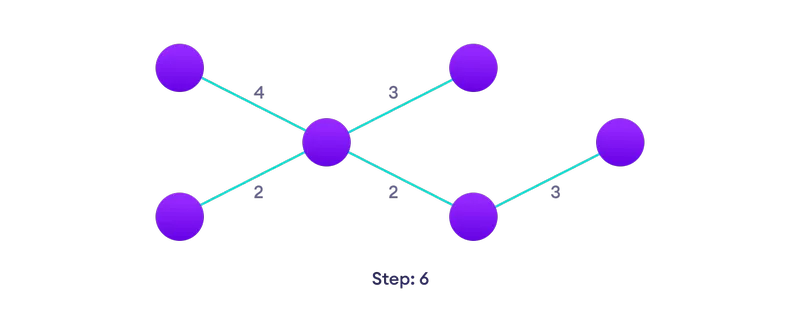

Lặp lại cho đến khi bạn có một cây bao trùm

Mã giả thuật toán của Prim

Mã giả cho thuật toán của prim cho thấy cách chúng ta tạo hai tập đỉnh U và VU. U chứa danh sách các đỉnh đã được thăm và VU danh sách các đỉnh chưa được thăm. Từng cái một, chúng ta di chuyển các đỉnh từ tập VU sang tập hợp U bằng cách nối cạnh có trọng số nhỏ nhất.

 T = ∅; U = ( 1 ); while (U ≠ V) let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U; T = T ∪ ((u, v)) U = U ∪ (v)

Ví dụ về Python, Java và C / C ++

Mặc dù sử dụng biểu diễn ma trận kề của đồ thị, thuật toán này cũng có thể được thực hiện bằng cách sử dụng Danh sách kề để cải thiện hiệu quả của nó.

Python Java C C ++

 # Prim's Algorithm in Python INF = 9999999 # number of vertices in graph V = 5 # create a 2d array of size 5x5 # for adjacency matrix to represent graph G = ((0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)) # create a array to track selected vertex # selected will become true otherwise false selected = (0, 0, 0, 0, 0) # set number of edge to 0 no_edge = 0 # the number of egde in minimum spanning tree will be # always less than(V - 1), where V is number of vertices in # graph # choose 0th vertex and make it true selected(0) = True # print for edge and weight print("Edge : Weight") while (no_edge  G(i)(j): minimum = G(i)(j) x = i y = j print(str(x) + "-" + str(y) + ":" + str(G(x)(y))) selected(y) = True no_edge += 1

 // Prim's Algorithm in Java import java.util.Arrays; class PGraph ( public void Prim(int G()(), int V) ( int INF = 9999999; int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false boolean() selected = new boolean(V); // set selected false initially Arrays.fill(selected, false); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in // graph // choose 0th vertex and make it true selected(0) = true; // print for edge and weight System.out.println("Edge : Weight"); while (no_edge < V - 1) ( // For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise // choose another vertex nearest to selected vertex at step 1. int min = INF; int x = 0; // row number int y = 0; // col number for (int i = 0; i < V; i++) ( if (selected(i) == true) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) System.out.println(x + " - " + y + " : " + G(x)(y)); selected(y) = true; no_edge++; ) ) public static void main(String() args) ( PGraph g = new PGraph(); // number of vertices in grapj int V = 5; // create a 2d array of size 5x5 // for adjacency matrix to represent graph int()() G = ( ( 0, 9, 75, 0, 0 ), ( 9, 0, 95, 19, 42 ), ( 75, 95, 0, 51, 66 ), ( 0, 19, 51, 0, 31 ), ( 0, 42, 66, 31, 0 ) ); g.Prim(G, V); ) )

 // Prim's Algorithm in C #include #include #define INF 9999999 // number of vertices in graph #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight printf("Edge : Weight"); while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) printf("%d - %d : %d", x, y, G(x)(y)); selected(y) = true; no_edge++; ) return 0; )

 // Prim's Algorithm in C++ #include #include using namespace std; #define INF 9999999 // number of vertices in grapj #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight cout << "Edge" << " : " << "Weight"; cout << endl; while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) cout << x << " - " << y << " : " << G(x)(y); cout << endl; selected(y) = true; no_edge++; ) return 0; )

Thuật toán của Prim vs Kruskal

Thuật toán Kruskal là một thuật toán cây bao trùm tối thiểu phổ biến khác sử dụng một logic khác để tìm MST của một đồ thị. Thay vì bắt đầu từ một đỉnh, thuật toán của Kruskal sắp xếp tất cả các cạnh từ trọng số thấp đến cao và tiếp tục thêm các cạnh thấp nhất, bỏ qua những cạnh tạo ra chu trình.